 It's either all wrong, or it is one of the most important theoretical physics discoveries in history, a major step in the direction of a unified field theory.
It's either all wrong, or it is one of the most important theoretical physics discoveries in history, a major step in the direction of a unified field theory.
In An Exceptionally Simple Theory of Everything, one Garrett Lisi, physics Ph.D and, yes, nearly-homeless surfer dude, suggests that E8 (described by the UK Daily Telegraph as an “eight-dimensional mathematical pattern with 248 points first found in 1887, but only fully understood by mathematicians this year after workings, that, if written out in tiny print, would cover an area the size of Manhattan”) has this amazing property: E8, says, Dr. Lisi, contains the Standard Model, plus the symmetries belonging to gravity.
And, oh yes, the model makes the testable hypothesis that there are 20 more standard particles waiting to be found by supercolliders. (Twenty seems like rather a lot?)
Here's the abstract of the paper,
Abstract: All fields of the standard model and gravity are unified as an E8 principal bundle connection. A non-compact real form of the E8 Lie algebra has G2 and F4 subalgebras which break down to strong su(3), electroweak su(2) x u(1), gravitational so(3,1), the frame-Higgs, and three generations of fermions related by triality. The interactions and dynamics of these 1-form and Grassmann valued parts of an E8 superconnection are described by the curvature and action over a four dimensional base manifold.
This representation, to the very limited extent I follow it, doesn't tell us anything directly about the shape of the universe; rather it threatens to tell us something fundamental about the relationships between the particles and forces that make up and that shape the universe. While the “exceptionally simple” part of the paper title is — or had better be — a joke, the 248 dimensions of E8 are needed only for representation of relationships; the universe it describes has only the three dimensions we know, plus time, distinguishing this theory from string theory, which requires many more (even if some are very tiny).
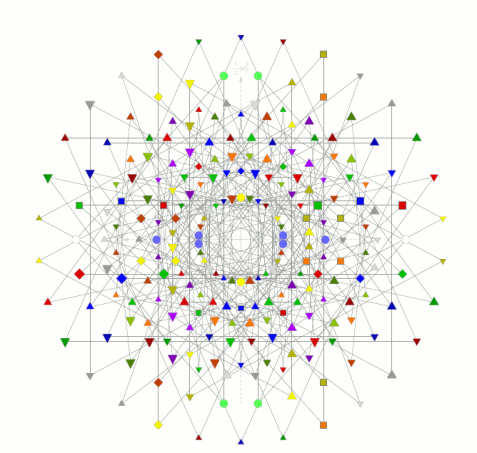
Dr. Lisi's theory also makes pretty pictures.
Pictured above: figure 2 of Dr. Lisi's paper, “The E8 root system, with each root assigned to an elementary particle field.” There's also a cute movie of an E8 being rotated.
As noted above, there are already critics. Super-string advocate (and politically weird) Luboš Motl will have none of it.
He blogs,
The author is not constrained by any old “conventions” and simply adds Grassmann fields together with ordinary numbers i.e. bosons with fermions, one-forms with spinors and scalars. He is just so skillful that he can add up not only apples and oranges but also fields of all kinds you could ever think of. Every high school senior excited about physics should be able to see that the paper is just a long sequence of childish misunderstandings.
…
If you care how the forces and particles are supposed to be embedded into his group, it's like this. You start with a non-compact real form of E8. You embed a G2 into it. Its centralizer is a non-compact version of F4. Now, you embed the strong SU into the G2 while the non-compact F4 acts as the source of a “graviweak” SO group that contains SO, a “gauge group” that is now fashionable in the crackpot circles to “describe” gravity, and SO, their source of cargo cult electroweak symmetry.
Of course, this group plays a different role (in the vielbein formulation of general relativity) than the Yang-Mills groups and the fact that these two kinds of a group cannot be merged is the content of the Coleman-Mandula theorem to be discussed at the end of my text. Moreover, the fermions clearly can't arise from the connection because they have a different spin and statistics and they don't transform in the adjoint representation. For people like A. Garrett Lisi, it is not hard to unify everything with everything else because they don't know any difference between different concepts in physics.
You might think that the E8 starting point is analogous to heterotic GUTs. Except that it is completely crucial for physics that E8 in heterotic string theory is compact. Non-compact gauge groups would lead to ghosts and negative probabilities. Moreover, the whole Standard Model is embedded into the same subgroup of the heterotic E8 once it's broken, e.g. to SO. Also, everyone knows that the fermions arise as chiral multiplets and not vector multiplets: they are simply not and cannot be a part of the gauge bundle. Most importantly, no sane person has ever claimed that the E8 portion of the heterotic theory already contains gravity. That would be really silly.
So what we have here is either the theoretical physics equivalent of cold fusion, or one Czech physicist who will become unwittingly famous.
More at slashdot.
